现在很多大语言模型（LLM）经常给出看似正确的结论，可一看过程，就让人直摇头。那么，这些模型真的理解了推理过程吗？还是只是看起来“像那么回事”就蒙出来的 ？

不等式问题是检验模型“真会不会证明”的理想对象——结构简单、逻辑清楚，又特别容易暴露出推理过程中的漏洞。可以说，它们就像是 AI 数学推理能力的“照妖镜”。

而想要探究该问题所面临的核心挑战，其实就是现在形式化数学努力解决的事：验证推理过程的严谨性。比如 Lean、Coq 这种形式化系统，就能够无差错的验证证明过程的正确性。但是他们对逻辑的要求极高，每一步都得写得规规矩矩，计算机才能验算。这些系统门槛高、自动化低，写起来累人不说，遇到奥数级别的不等式题，还很难实现规模化处理。

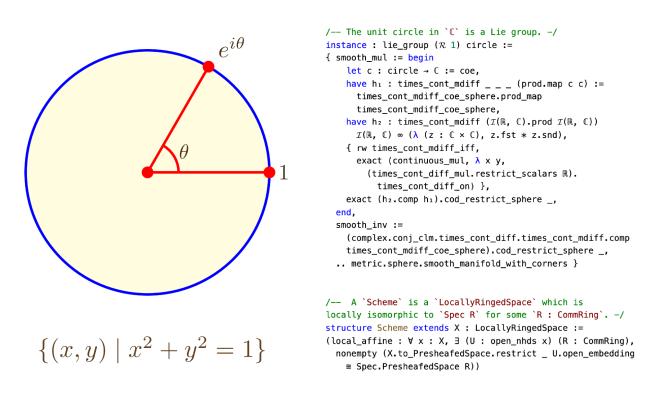
Lean 语言用于进行数学证明的示例图

反过来看，大语言模型是用大量自然语言训练出来的，虽然直接生成机器可验证的形式化证明的能力并不是太强，但在“非正式推理”这块反倒表现不错。同时自然语言符合人类的思考模式，门槛低，易处理。因此，探索大语言模型在自然语言环境下进行不等式证明的能力，是一个既有趣又具有重要研究价值的课题。

于是，斯坦福、伯克利和 MIT 的研究团队提出了一个新思路：把不等式证明拆成两个用非正式的自然语言写成的但可以验证的小任务——“界限估计”和“关系预测”。在这套框架下，他们还构建了一个全新的 benchmark 数据集，叫 IneqMath。它等于是在自然语言和形式化逻辑之间，搭建了一座“中间桥梁”，可以一步步在自然语言的环境下检查模型的推理过程，判断它是真的在“讲理”，还是又在蒙。

项目主页：https://ineqmath.github.io

论文：https://arxiv.org/abs/2506.07927

代码库：https://github.com/lupantech/ineqmath

数据集：https://huggingface.co/datasets/AI4Math/IneqMath

排行榜：https://huggingface.co/spaces/AI4Math/IneqMath-Leaderboard

这套“非正式”方法怎么评估证明？ 

简单来说，他们把一个不等式题分成两个小任务： Bound Estimation（估计上下限）和 Relation Prediction（关系预测）。比如，对于一个证明问题：

对于任意实数 a，b，请证明 a^{2}+b^{2}geq 2ab，就可以转化成对应的这两个小任务：

Bound Estimation（估计上下限） 

对于任意实数 a，b，请判断两个式子的关系：a2+b2? 2ab

Relation Prediction（关系预测）

对于任意实数 a，b，请求出最大的常数 C 使得 a2+b2 ≥ Cab 恒成立。

这两类任务可以直接用自然语言 +LaTeX 来表达，大模型也能按步骤做题，既保留了数学题目的可证明性，又不用搞得太复杂。同时，答案是唯一的，验证也方便。

IneqMath：首个“自然语言但可验证”的不等式数据集 

研究团队在上述任务结构的基础上构建了 IneqMath 数据集。该数据集包含 1,252 道不等式题目作为训练集，每道题目均配有详细的解答过程和相关定理的标注。同时，数据集还包含由国际数学奥林匹克金牌选手标注的 200 道测试题，以及 100 道验证题。

以下是 IneqMath 的训练和测试题目示例：

怎么判断模型推理到底靠不靠谱？ 

研究团队为此专门设计了一套“AI 数学裁判系统”，名字虽然没那么花哨，但功能超实用——它不仅可以判断最终答案是否正确，还能从四个不同的角度自动评估模型的每一个推理步骤是否合逻辑，避免只看最终答案被“蒙对”所欺骗。以下是四个从不同角度评判过程严谨性的评审器：

• Toy Case Judge：判断是否用特殊值推断出一般的结论，忽略了泛化过程.
• Logical Gap Judge：判断是否存在跳步、未解释的等价变形等逻辑偏差
• Numerical Approximation Judge：判断是否存在不当近似
• Numerical Computation Judge：判断计算是否正确，包括基本代数运算或代入过程中的数值错误

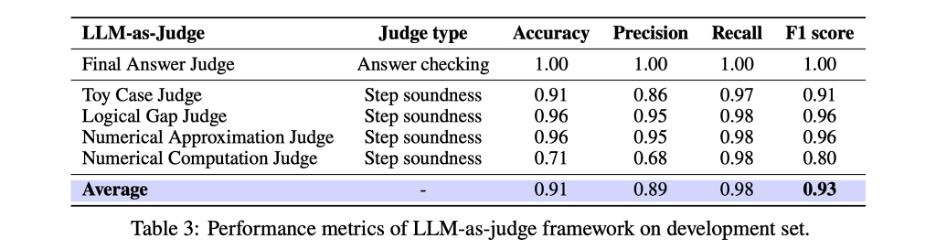
准确率高达 F1 = 0.93，人类都能下岗？ 

这套系统不是只“挑刺”，它的准确率也非常高。研究团队用人工标注结果做了对比，发现这些自动评审器在判断是否严谨这件事上，和人类专家的判断一致性非常高，F1 值达到了 0.93！简单说，它已经可以非常可靠地替代大量人工审卷的工作。

一些关键发现 

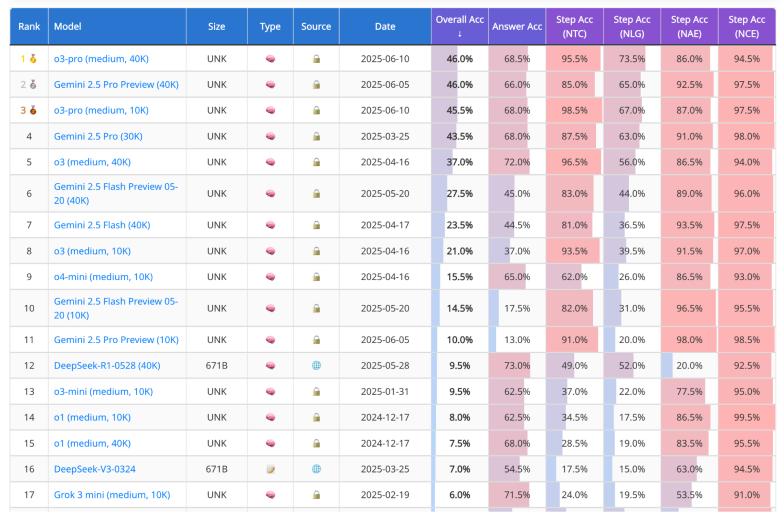
“答案准”≠“推得对” 

很多时候，大语言模型能给出正确答案，但过程根本经不起推敲。以 Grok 3 mini 为例，它在测试中，最后给出的答案有 71.5% 是对的，听起来挺厉害吧？但问题来了：研究团队用他们那套自动评审系统一评审——结果只剩下 6% 的答案是“过程合理、逻辑严谨”的。而且这个问题不是 Grok 一家独有，几乎所有模型都出现了类似的情况，“准确率”最多掉了 65.5%。这说明很多模型虽然能“猜”到答案，但推理过程要么跳步了、要么靠代值、要么干脆就是模糊解释蒙混过关。

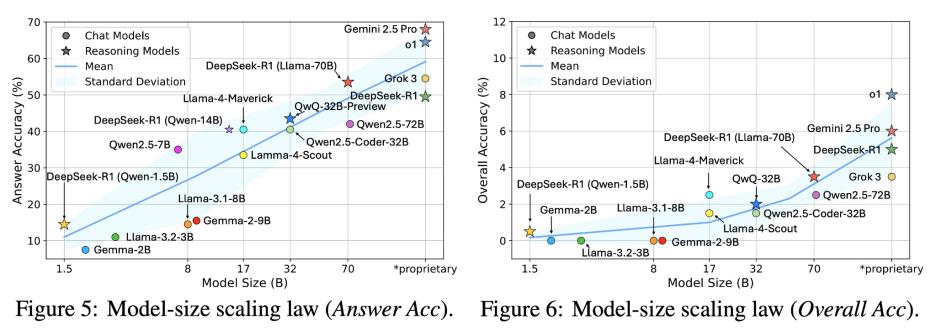
模型大了，推理就更好吗？不一定！ 

大家总觉得模型越大，智商就越高，是不是？在一定程度上没错——研究发现，大模型确实更擅长“猜答案”，在各种数学题上，答案准确率往往是随着参数量稳步提升的。但当我们不光看答案，而是深入去评估 推理过程是否严谨 时，这个“变强”的趋势就停了下来。

所以，靠加参数堆硬件这条路，在提升推理严谨性这件事上是走不通的。逻辑和严谨性不是模型大就能自动长出来的。

想得多，不代表想得对 

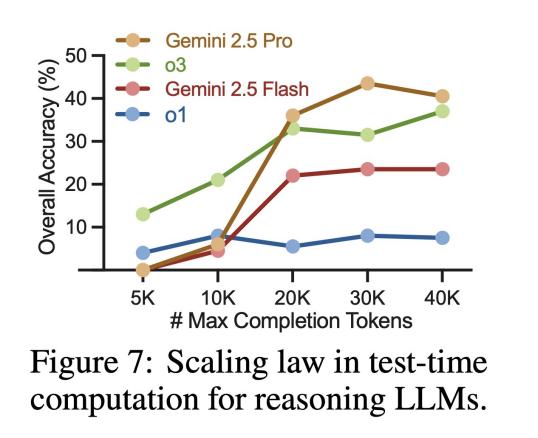
那我们换个策略：让模型“想久一点”，是不是效果会更好？也就是让它用更多 token、写更长的推理过程，慢慢分析是不是能更靠谱？

结果证明……也不是特别管用。

研究团队试着放宽限制，让模型生成更多内容，虽然推理的严谨性 略有提升，但很快就进入了“瓶颈区”——无论你再多给它多少 token，提升都很有限。推理长度增加，质量却没同步跟上。

就像学生考试时，如果不会做题，写再多废话也不会得分；关键还是得答到点子上。大模型也是一样，“想得多”不代表“想得清楚”。

两个有效办法 

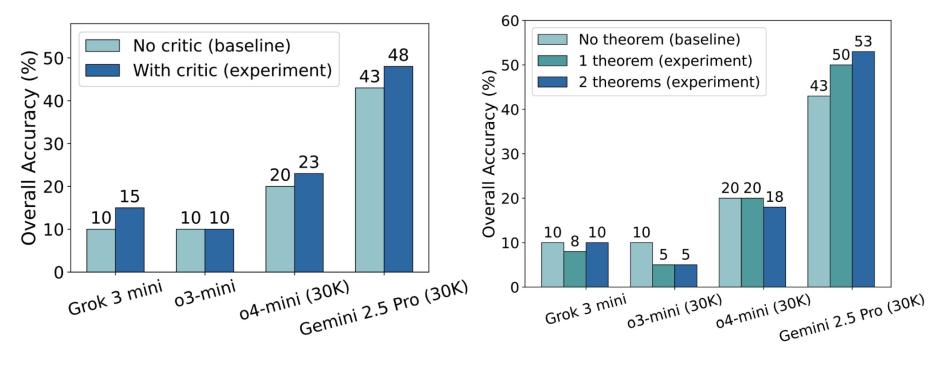
虽然大模型证明推理还不太行，但研究团队发现两个方法确实有效：

自我批判（Self-Critique）

让模型先审一遍自己，再改答案。像学生检查作业一样，这招让 Gemini 2.5 Pro 的准确率提升了 约 5%。

定理提示（Theorem as Hints）

提前喂给模型相关定理，就像考前划重点。结果准确率最多提升 10%，尤其对复杂题特别有帮助。

说明只靠算力不够，教会模型“自我反思”和“用工具”，才是真正变聪明的路。

结    语 

现在的大模型会猜，但还不太会严格推理。IneqMath 不是来证明模型都不行的，而是帮它一步步学会怎么推理，怎么变成一个真正会“证明”的数学 AI。

也许今天它还只是“猜得好”，但未来，它有可能真的“想得明白”。