今日，首个达到国际数学奥林匹克竞赛（IMO）银牌水平的人工智能（AI）模型——AlphaProof，登上了权威科学期刊 Nature。

论文链接：https://www.nature.com/articles/s41586-025-09833-y

去年，Google DeepMind 凭借 AlphaProof 这一奥赛级人工智能模型，引发了学界轰动，被业内比喻为“登月”时刻。

据论文描述，AlphaProof 这一成果证明了“自动化系统已具备攻克传统认为无法解决的数学难题的能力”，不仅是技术层面的里程碑，也为“可验证的机器推理”提供了可行路径。

新闻与观点文章链接：https://www.nature.com/articles/d41586-025-03585-5

在同期发表的新闻与观点文章中，伊利诺伊大学厄巴纳-香槟分校助理教授 Talia Ringer 表示：

AlphaProof 是她所用过的第一款“真正实用的 AI 工具”，拥有着“高度可靠”的证明质量，每一步的推理都能获得来自证明辅助工具的即时反馈，从而避免了自然语言推理中常见的模糊与错误，这一点是自然语言模型所不具备的。

“尽管仍存在局限性......但可以肯定的是，这个领域正在发生深刻变革，AlphaProof 或许正是未来趋势的先行者。”

AlphaProof：首次实现奥数级形式化推理

训练能够在复杂、开放环境中进行有效推理并找到解决方案的智能体（Agent），是人工智能研究面临的关键挑战之一。

数学，尤其是奥数题目，要求创造性思维和多步推理能力，因此被视为衡量高级智能体能力的标准化评估场景。

在这项工作中，研究团队延续了先前在 AlphaZero 等系统中的思路：通过强化学习让智能体在规则明确的环境中进行自我博弈与改进；不同的是，这一次的“棋盘”不再来自围棋或国际象棋，而是数学定理本身。

在具体实现上，AlphaProof 将数学定理证明过程转化为一个强化学习任务。在 Lean 定理证明器环境中，每一次证明过程都会被定义为状态、动作与奖励，通过不断尝试与反馈，学习如何将假设转化为结论，逐步形成稳定的推理策略。

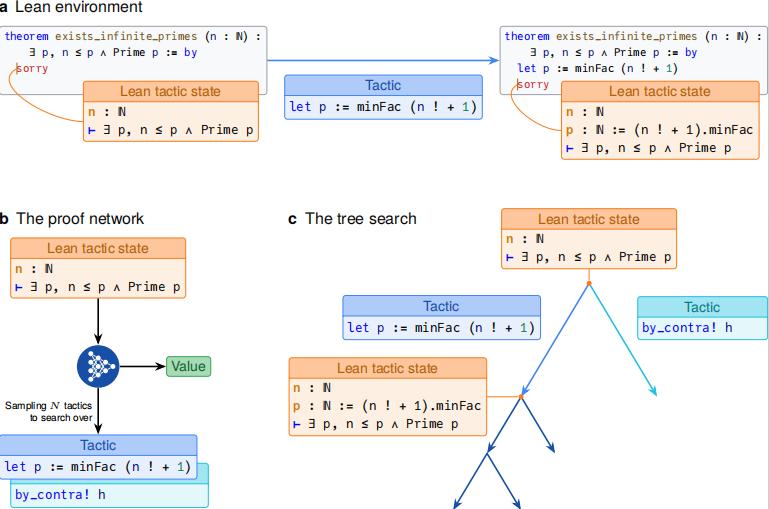
图｜AlphaProof 核心推理组件

AlphaProof 的训练过程分为多个阶段。首先，模型在约 3000 亿 token 的数学与代码语料上进行预训练，以学习符号逻辑、语法和基础的数学语言表达结构。随后，研究者利用约 30 万条 Lean tactic 证明数据对模型进行监督微调，使其能够理解 Lean 的形式化语法与命令结构。

为了构建大规模训练数据，他们开发了基于 Gemini 模型的自动形式化系统，将自然语言题目转化为 Lean 的逻辑表达。该系统自动生成了约 8000 万个形式化数学问题，涵盖代数、数论、几何与组合数学等多个领域，成为 AlphaProof 强化学习的核心训练素材。

在主训练阶段，AlphaProof 系统在生成的问题上进行自我博弈式学习：不断尝试证明、验证结果、更新策略，并通过 Lean 核心验证结果的正确性，形成强化学习循环——每当系统找到正确证明时，就会获得正向奖励；若证明失败，则回溯并尝试新的路径，从而逐步掌握复杂的推理模式。研究团队称，这一过程累计消耗了约 8 万 TPU 天的计算资源。

在推理阶段，研究团队提出了“测试时强化学习”（TTRL）机制，当AlphaProof 遇到难度较高或从未见过的题目时，会围绕目标问题临时生成数千个结构相似的变体，在这些变体上进行短期自我强化学习，然后将更新后的策略应用回原题求解。

这种“临场学习”的方法显著增强了模型的泛化与解决新题的能力：实验结果显示，TTRL 让系统的解题率在多项基准上提升了约 10%–15%。

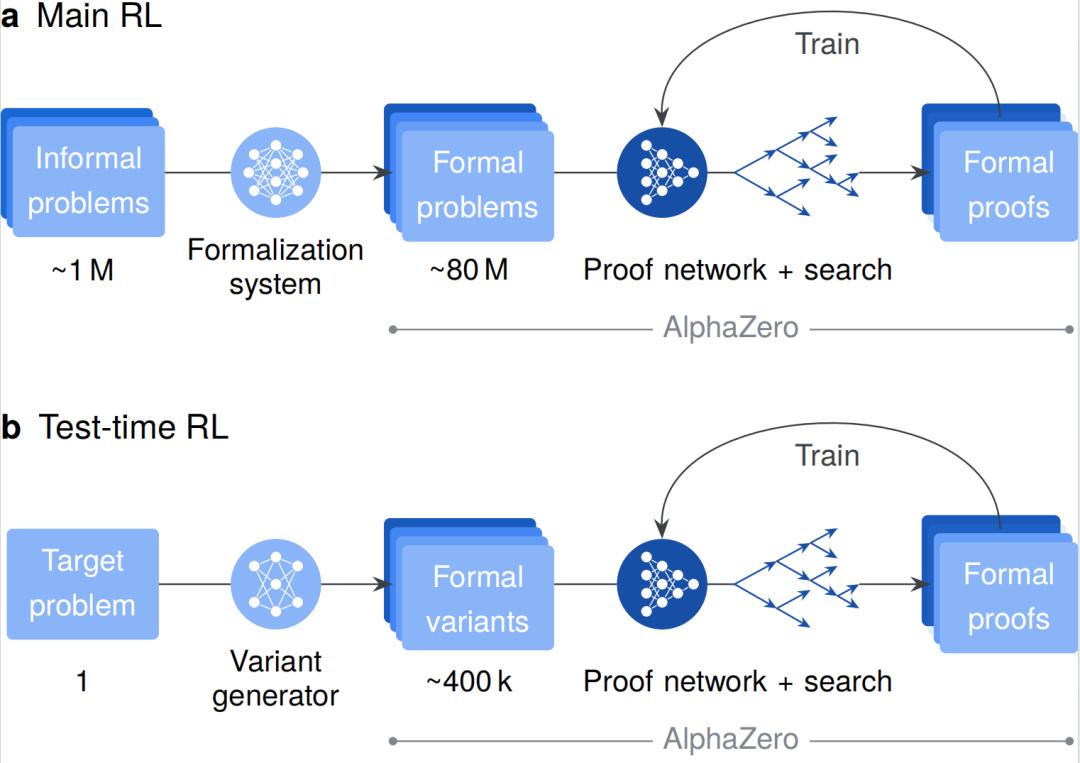
图｜AlphaProof 学习与自适应流程

从结果上看，AlphaProof 在多个数学推理基准测试上展现出了领先的性能。在 miniF2F、PutnamBench、formal-IMO 等形式化数学基准测试上的结果，均证明了 AlphaProof 在定理证明成功率和搜索效率方面达到了 SOTA 水平。

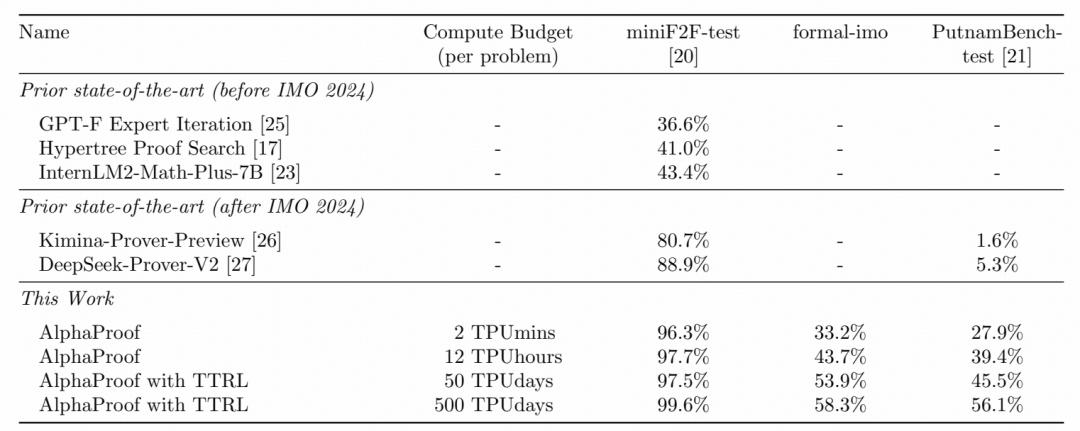
图｜AlphaProof 在多个形式化数学基准测试的表现

在 2024 年的国际数学奥林匹克 IMO 模拟测试中，AlphaProof 的表现尤其令人瞩目——成功独立证明三道非几何题（P1、P2、P6），其中包括整场最难的题目 P6。

图｜AlphaProof 完整解答 IMO 2024 数学竞赛第一题的证明过程

与此同时，Google DeepMind 的另一个系统 AlphaGeometry 2 则负责解决几何题。两者合计得到 28 分（满分 42），相当于人类参赛者的银牌水平。

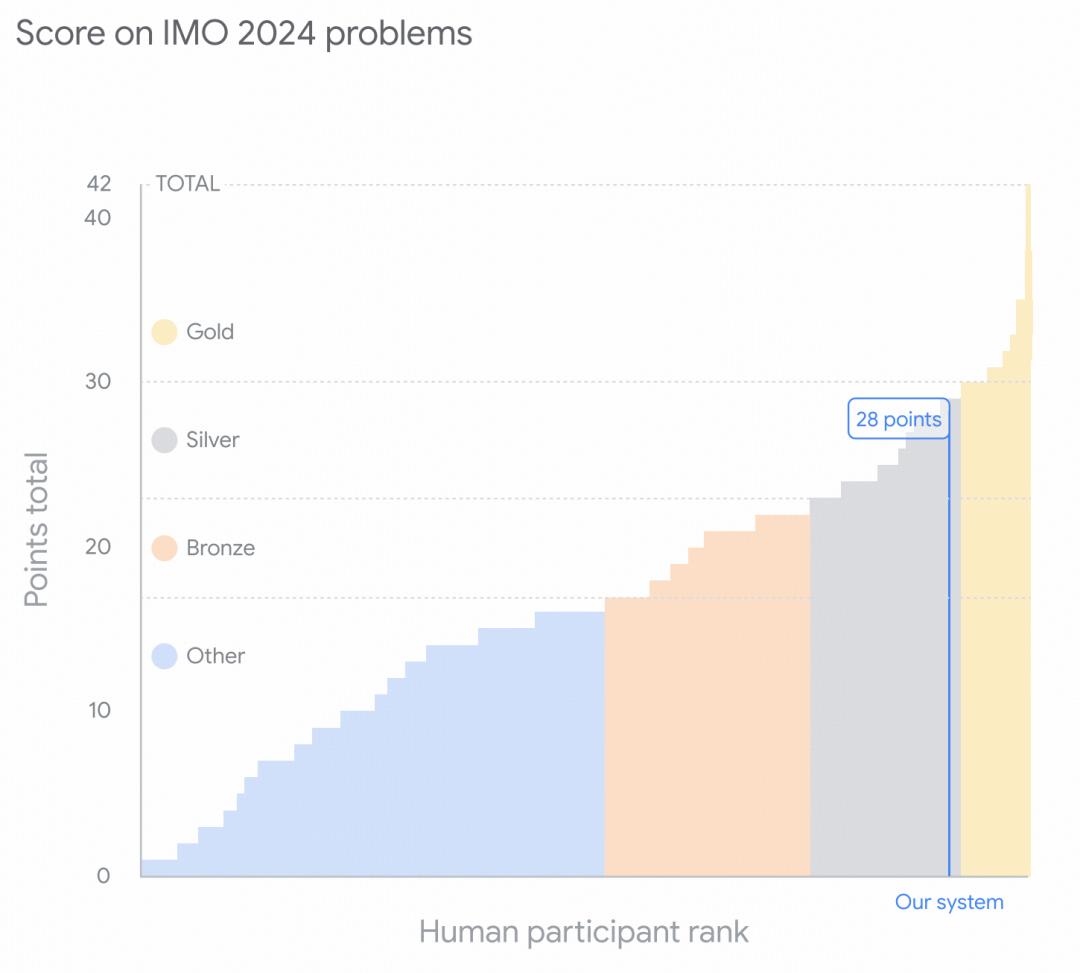
论文指出，这是人工智能首次在国际数学奥林匹克上达到奖牌水平，与先前只能解决中学或大学低年级题目的系统相比，AlphaProof 的表现“展示了基于经验学习的形式化系统在复杂推理领域的潜力”。

迈向可验证科学智能

在论文的讨论章节，研究团队强调，AlphaProof 的核心贡献在于证明了强化学习可以与形式化逻辑系统结合，从而实现高水平的可验证数学推理。

与基于自然语言模型的推理不同，AlphaProof 的每一步逻辑均通过 Lean 的验证器审查，这种“形式化可验证”的方法，为人工智能在科学推理和理论研究中的应用奠定了重要基础。

研究团队也坦言，AlphaProof 也同样存在一些局限，包括：训练与推理的计算成本高；推理速度慢，TTRL 阶段常需数天计算时间；仍难以处理开放性、创造性极强的数学问题。

尽管如此，研究团队认为，这一成果展示了人工智能系统向更高层次推理能力迈进的可行路径。

在未来工作中，他们将重点优化模型效率、降低算力需求，并进一步探索形式化学习在数学与其他科学领域中的应用。

此外，他们还计划开发交互式工具，使研究人员能够直接与系统协作，让人工智能成为“科学探索的合作者”。