GPT-5正改写科学发现的规则!一篇重磅论文揭秘,「量子版NP难题」竟被GPT-5在30分钟之内攻克了,然而这要耗费人类1-2周的时间。照这种速度发展下去,AI离完成「诺奖级」突破真的不远了。
几天前,GPT-5成功通过「哥德尔测试」,破解了数学三大猜想。
意想不到的是,这一次,GPT-5又「攻陷」了量子领域的难题。
量子计算专家Scott Aaronson首次发表论文,证明其中一个老难题竟被GPT-5助攻破解了。
论文中,Scott一直在死磕量子计算中的一个核心问题——QMA复杂度类别,堪称「量子版的NP问题」。
其中,关键在于证明过程中的误差概率,能否被无限降低,特别是,能否实现完美完备性。

论文地址:https://arxiv.org/pdf/2509.21131
之前学界研究中已经把误差压到很低,但最新研究却发现:「双指数级误差」是现有方法的理论极限,无法进一步突破。
在关键推导环节受阻后,作者开始向GPT-5寻求帮助。一开始,AI给出了错误的思路。
但在大约30分钟交互后,它最终提出一个精妙的数学函数,精确分析出特征值行为。
研究证明,这一构想成为了论文中最关键的突破。
在最新博文中,Scott惊叹地表示,「这思路要是哪个学生想出来的,我绝对会夸一句——真是绝了」!

这个难题预估需要1-2周人力才能完成
OpenAI科学家Sebastien、产品负责人Kevin再次激动转发,并称「一场重大变革开始了」。



量子版NP难题:QMA奇点
这篇于25日提交至arXiv的论文,主要研究了量子复杂性类「QMA中黑盒放大的局限性」。

那么,QMA是什么?
QMA,即量子梅林-亚瑟(Quantum Merlin Arthur),可以看作是NP的典型量子版本。
它包含了一类决策问题:
如果答案是「是」,Merlin可以发送给Arthur一个量子见证态,能让Arthur(在经过多项式时间的量子计算后)以至少2/3的概率接受;
而如果答案是「否」,无论Merlin发送什么见证态,Arthur接受的概率都至多为1/3。

在这里,如同复杂性理论中常见的那样,常数2/3和1/3只是惯例,可以通过放大替换为,比如1-2⁻ⁿ和2⁻ⁿ。
在这个领域,一个长期悬而未决的问题是——
QMA是否等于QMA₁,其中QMA₁是QMA的一个子类,允许协议具有「完美完备性」?
2008年,Scott Aaronson通过实用分析方法,证明了存在一个「量子预言机」,使得QMA≠QMA₁。
这意味着,任何证明QMA=QMA₁的尝试,都需要「量子非相对化技术」。
这倒并不是说这个障碍难以逾越,但至少说明了问题的复杂性。

突破:双指数放大局限
直到今年6月,Freek Witteveen和Stacey Jeffery发表了一篇重磅论文,证明了QMA协议可通过黑盒方式放大,让完备性误差达到了「双指数级小」,即 1/exp(exp(n))。

论文地址:https://arxiv.org/pdf/2506.15551
他们采用了一种Scott从未想过的方法:将接受概率编码到一个量子态的振幅中,而这些振幅以几何级数递减。
事实证明,QMA这位相识25年的「老朋友」,依然能带来惊喜。
在8月的线上会议,Scott问道:
这个双指数的完备性,是黑盒技术的极限吗?能否进一步放大到三指数级小,即1/exp(exp(exp(n)))。
30分钟攻克,GPT-5上大分
一周后,Scott联手Freek写出了完整证明,表明在黑盒技术下,双指数级小的完备性误差已是极限。
换句话说,他们将2008年的「QMA≠QMA₁」预言机分离结果量化,得到的「下界」(lower bound)恰好与6月论文的协议相匹配。

这项研究最引人注目的部分,或许并不是量子复杂性本身,而是AI在其中的角色。
如前所述,这是Scott Aaronson第一篇论文,其主要成果证明中的一个关键技术步骤来自AI。
具体来说,是GPT5-Thinking。

当时,作者面临的一个问题是:分析一个N×N的厄米矩阵E(θ)(比如,N=2ⁿ),其每个元素都是一个关于实参数θ的poly(n)次三角多项式。
需要证明的是,当θ从0变化到1时E(θ)的最大特征值,以证明λₘₐₓ(E(θ))不可能从一个接近0的值开始,然后长时间「停留」在接近1的状态,例如接近 1/exp(exp(exp(n)))。
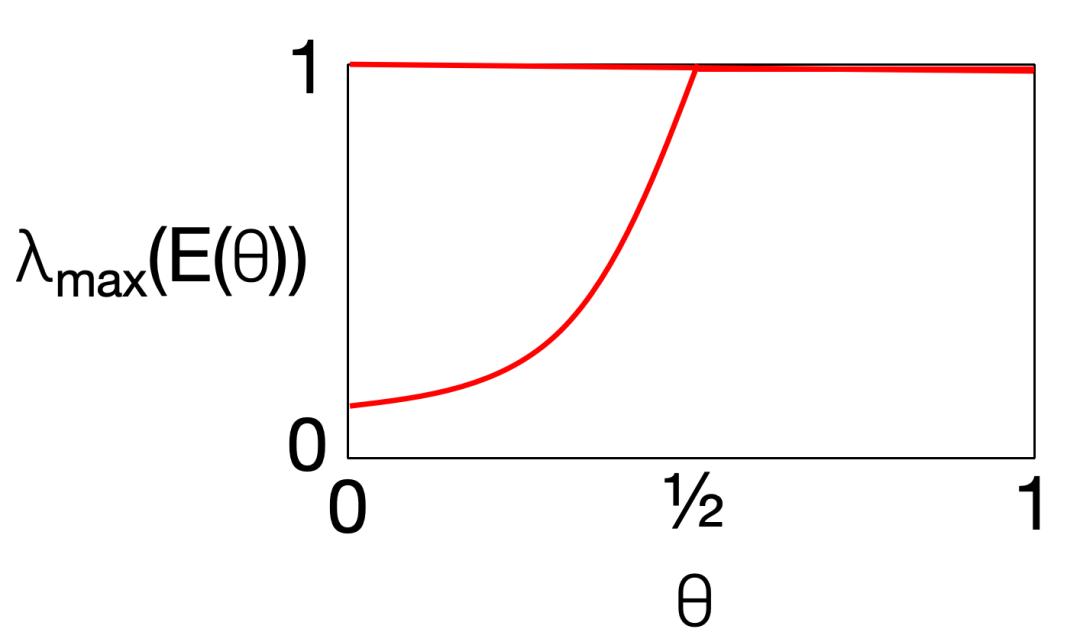
针对这一问题,如有1-2周的时间,Scott和合著者查阅文献也可以解决。
但他选择了GPT5-Thinking,5分钟后,它给出了一个自信但明显错误的答案。
Scott并没有嘲笑AI,而是告诉它错在哪里。GPT5-Thinking在思考片刻后,再次尝试给出了一个更好的方案。
就这样,经过了几次反复迭代,如同研究生/同事交流一样,GPT-5给出了以下函数:
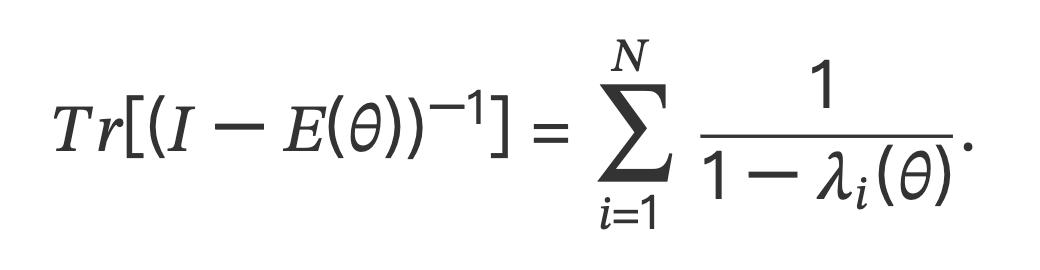
它正确指出,这是一个关于θ的次数可控的有理函数,并且恰好编码了最大特征值 λₘₐₓ(E(θ))与1的接近程度的相关信息。
令人欣喜的是,这个方法奏效了,不用AI协助就能轻松完成验证。
Scott认为,或许GPT5在训练数据中,某个地方见过类似结构,但若是学生提出的方案,他会毫不犹豫地称其为「巧妙」。
最后,他回忆道,一年前,自己曾用当时的GPT推理模型尝试类似问题,结果远不如人意。
现在,是2025年9月,我可以明确告诉你——
AI已经开始真正触及那些我认为最具人类智慧特征的核心工作:证明量子复杂性类之间的预言机分离。
虽然它现在还做不到独立撰写整篇研究论文,但如果你清楚自己在做什么,它能帮你摆脱困境,这可以说是一个绝佳的应用场景。
谁知道,这种情况会持续多久?
Scott Aaronson调侃道,「想到这儿,不禁庆幸自己还有个铁饭碗——终身教职」。
参考资料:
https://scottaaronson.blog/?p=9183
https://x.com/SebastienBubeck/status/1972368891239375078
https://x.com/kimmonismus/status/1972399015825203463



